第3回 平面図形・角度
小林講師(中学受験鉄人会スーパープロ家庭教師)
早稲田中において、たいへん出題率の高い平面図形・角度を求める問題についてお話させていただきます。角度の問題は大きく分けて3つのパターンになります。1つは図形を折ってできる角度を求める問題。2つめは図形を重ねてできる角度を求める問題。3つめは補助線などをひいて角度をもとめる問題です。
■ 図形を折ってできる角度をもとめる問題
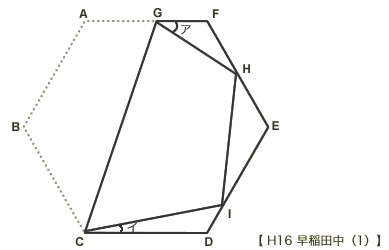
正六角形の紙を次の図のように1つの頂点が辺の上に重なるように折り曲げました。アの角度とイの角の大きさの和は何度ですか。
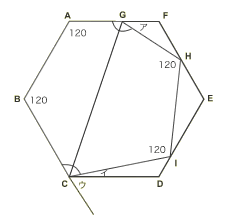
GCを軸に折ったので四角形ABCGと四角形HICGは線対称な図形になります。正六角形ABCDEFなのでLGAB=LABC=LGHI=LHIC=120度。そして、LAGH+LBCIの大きさは六角形ABCIHGより、720−120×4=240度と分かります。正六角形の外角ウをつくり、ア+イ+ウを考えます。
ア+イ+ウ=180度×2−(LAGH+LBCI)
=360度−240度
=120度
ウ=60度より、ア+イ=120度−60度=60度になります。
■ 図形を重ねてできる角度をもとめる問題
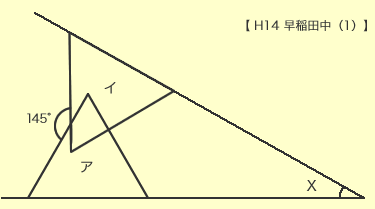
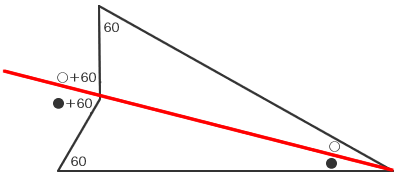
次の三角形(ア)と三角形(イ)はどちらも正三角形です。Xの角度は何度ですか。
三角形(ア)、三角形(イ)は正三角形なので、図のように角度が分かります。そして五角形に対して補助線を引いて考えます。
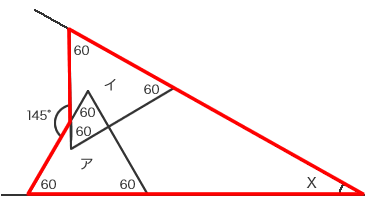
Xの大きさを○+●としてあらわすと
角度の定理により
○+60度+●+60度=145度
○+●=145-60-60
○+●=25度 と分かります。
早稲田中の算数において角度の問題は必修です。どのように導き出すか。そのチカラを大切にしているのが早稲田中の算数だと思います。解き方も1つではありません。いろいろな方法を考えながら学習して下さい。また、正三角形や正五角形はよく使われます。角度・面積の分割などです。充分に慣れておいて欲しいと思います。












