第4回　基準量をそろえる｜線分図の究極奥義｜中学受験！パパとママの勉強部屋

第4回　基準量をそろえる

斎藤講師（鉄人会スーパープロ家庭教師）

　いよいよ基準量をそろえる問題に入ります。もとにする量がいくつかでてきて，もとにする量をそろえることで問題を解いていきます。今後取りあげる予定となっている比をそろえる場合と異なり，分数・小数の割合は整数にならないため，とっつきにくい印象を持ちやすいことが多いです。加えて，大部分の教材では分数・小数の関係とその計算を扱うとき，中途半端に割合を導入するために，学習の理解を大いに妨げています。分数・小数の計算を十分習得した上で割合を学ぶのがよいでしょう。

　今回は残相当と分配算の問題を解きながら，割合関係だけの問題を理解して，分配算でそれを利用するという具合に進めていきます。今回の内容が割合のもっとも重要な部分といってもいいでしょう。逆に言えば，基準量をそろえる問題を確実に理解できれば，比の性質や割合と比が両方出てくる問題もそれほど抵抗なく理解できるでしょう。

　今回の割合とは関係ありませんが，特に計算問題の正答率が悪いという人について，その対策について考えてみましょう。次のようなことに注意して，毎日計算をやるようにしましょう。

（１）　計算する前

（ア）　鉛筆のこさをちょうどよいものを使うこと。
→こすぎたり，うすすぎたりせず，きちんとけずりましょう。
（イ）　鉛筆の持ち方を正しく持つこと
→鉛筆の先の方を持たないようにしましょう。
（ウ）　姿勢を正しくすること。
→机やいすの位置をちょうどよい高さにしましょう。
→足は床にしっかりとつけられるようにしましょう。

（２）　計算するとき

（ア）　数字を大きく，はっきりと書くこと。
→「０」と「６」をしっかりと区別しましょう。
→「１」を書くときはカギをつけないように書きましょう。
（イ）　筆算を消さずに残しておくこと
→筆算も式の１つです。別用紙に計算せず，その場に書きましょう。
→自分が正しいと思って書いたことは残しておきましょう。
（ウ）　カラー消しゴムでなく，プラスチック消しゴムを使うこと
→カラー消しゴムはよく消えません。
（エ）　計算の順番を必ず書くこと
→計算の順番と横の式を書き，筆算をその近くに書きましょう。

３）　計算したあと

（ア）　終わったらすぐにマルつけをすること
→ただし，バツはつけないでマルだけをつけましょう。
（イ）　まちえた問題のとき直しをすること
→マルにならなかった問題をもう一度解き直しましょう。

［例題１］残相当-基準量が変わる
　まりこさんは１２００円のおこづかいのうち，はじめに持っているお金のを貯金して，次に残りのでペンを買いました。これについて，次の問いに答えなさい。

（１）貯金したお金は何円ですか。

（２）ペンの値段は何円ですか。

［解説］
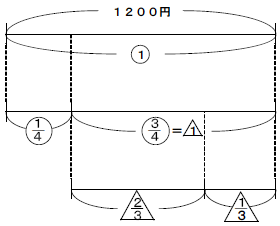
問題文にある２つの割合は今までと違い，もとにする量が異なります。最初に出てくるは最初に持っていた１２００円をもとにした割合で，次に出てくるは貯金をした後の残りのお金をもとにした割合です。もとにする量が変わるときは，その残りの部分をとおいてさらに線分図を書いていきます。

（１）をもとにする線分図をマルの線分図，をもとにする線分図をサンカクの線分図ということにします。マルの線分図は今までと同じなので問題はないでしょう。貯金したお金は１２００×＝３００円です。

（２）ペンの値段は貯金した３００円の残りの１２００-３００＝９００円をもとにした割合で考えなければなりません。マルの線分図でにあたる量を１とおいた新しいサンカクの線分図に書くと図のようになります。割合が出てきたら，必ずもとにする量をはっきりとさせることが大切です。ペンの値段は９００×＝６００円です。　　

［練習１］（解答はこの回の最後にあります。）
次の問いに答えなさい。（必ず線分図を書くようにしましょう）
（１）落とした高さのだけはね上がるボールがあります。５ｍの高さから落としたとき，３回目にはね上がる高さは何ｃｍですか。

（２）お年玉のを貯金しました。残りのお金で１８００円の人形を買いました。人形の金額は残りのお金のでした。お年玉を何円もらいましたか。

（３）ある本を５日かけて読みました。１日目に全体のを読み，２日目に残りの３割を読み，３日目には残りのを読み，４日目には残りのを読んだところ，５日目の分は１８ページになりました。この本は何ページありますか。

［例題２］余りの出る残相当
次の問いに答えなさい。
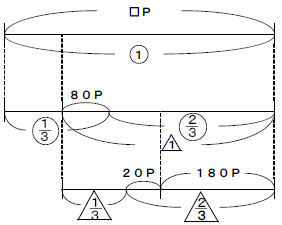
(1）ある本を１日目は全体のより８０ページ少なく，２日目に残りのより２０ページ多く読んだところ，１８０ページ残りました。この本は何ページありますか。

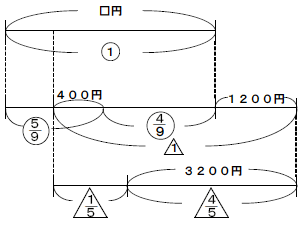
（２）あやこさんは昨日買い物にいき，所持金のより４００円安い値段でＴシャツを買いました。今日はお母さんにさらに１２００円もらって，３４００円の運動靴を買いました。運動靴の値段はそのとき持っていたお金のにあたります。最初の所持金は何円ですか。

［解説］
（１）「少ない」が出てきたら要注意です。基準量が変わる部分をまちがえないようにして線分図を書くと右のようになります。１８０＋２０＝２００ページがにあたるので，は２００÷＝３００ページです。３００-２０＝２８０ページがにあたるので・は２８０÷＝４２０ページになります。

（２）全体の量が変化して，もとにする量も変わる問題です。逆算して順に求めることもできますが，あくまで線分図でとらえる練習だと思って，しっかりと線分図を書けるようにしましょう。　　　　
３２００円が今日の所持金のにあたるのでは３２００÷＝４０００円になります。もらった２０００円を引いて４０００-１２００＝２８００円が昨日の残金になります。
　２８００-４００＝２４００円がにあたるので，は２４００÷＝５４００円になります。

［練習２］（解答はこの回の最後にあります。）
（１）サイクリングで目的地まで行きました。朝のうちに全体のより２．５ｋｍ少ない道のりを進み，休けいをしてから残りのより６ｋｍ多く進んだところ，目的地まで１．５ｋｍの地点まで来ました。出発地点から目的地までは何ｋｍですか。

（２）容器に水が入っています。全体のより３００ｍ少ない量を使ってから，１４０ｍを容器に足しました。さらにそのときの水の量のを使ったところ，残りの水の量は３９０ｍになりました。最初に入っていた水の量は何ですか。

［例題３］相当算-基準量をそろえる
次の問いに答えなさい。（１）１ｍのテープがあります。最初にテープ全体のを切り取って使い，次に残りのを切り取って使いました。いま残っているのは何ｍですか。分数で答えなさい。

（２）テープがあります。最初にテープ全体のを切り取って使い，次に残りのを切り取って使いました。いま残っているのは最初の長さのどれだけの割合ですか。分数で答えなさい。

［解説］
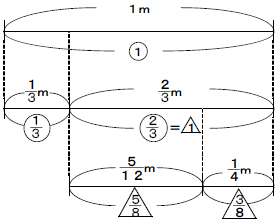
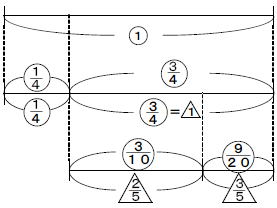
（１）線分図を書いてみると，例題１と変わりません。ただし，最初のもとにする量１ｍと割合のが同じ数になっています。最初に切り取ったテープの長さは１×＝ｍで，残りは１×＝ｍです。この残りを１とおきなおして，次に切り取ったのは×＝ｍで，いま残っているのは×＝ｍになります。このｍとｍはをもとにした割合を表していることが分かるでしょうか。つまりは，
のようにサンカクをマルで表せることになります。

（２）これがもとにする実際量がない，割合関係だけで考える問題です。もとにする実際量を１ｍとおけば（１）と同様になります。割合関係だけで考えにくいときは，もとにする量を自分でおいて考えることもできます。ここが前半の最も重要な部分です。理解できるまで繰り返しやるようにしましょう。線分図の書き方は実際量がないだけで今まで通りです。ただし，このときだけはマルの割合を線分図の上に書く禁じ手を使います。すると（１）のやり方でサンカクをマルで表せます。いま残っているのは最初の長さの×＝になります。

［練習３］（解答はこの回の最後にあります。）
（１）もらったおこづかいのうち，１日目に全体のを使い，２日目に残りのを使い，３日目にさらに残りのを使いました。２日目と３日目に使った金額の合計は全体のどれだけの

（２）もらったお年玉のうち全体の２０％を貯金し，残りの６割でおもちゃを買いました。いま持っているお金はもらったお年玉の何％ですか。

［例題４］分配算-基準量をそろえる
次の問いに答えなさい。
（１）みかんが全部で１８０個あります。このみかんをＡはＢの，ＣはＡのになるように分けると，Ｂは何個のみかんをもらいますか。

（２）色紙をＡ，Ｂ，Ｃ３人で分けました。ＡはＢよりＢのだけ多く，ＣはＡとＢの和のになるように分けました。Ａがもらった色紙は全体のどれだけの割合ですか。

［解説］
もとにする量の確認はできていますか。割合といえばもとにする量をはっきりさせることが大切です。

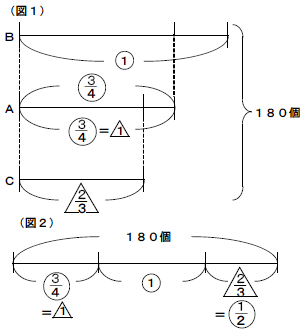
（１）差の線分図で割合関係を整理して，和の線分図で確認をしてみましょう。ＢとＡをそれぞれもとにする割合があるので，最初に出てきたもとにする量を，次に出てきたもとにする量をと表して図１のような線分図を書きます。
の関係があるのでＣのみかんの個数をマルで表すと，×＝になります。全体の１８０個にあたる割合は１＋＋＝２になるので，は１８０÷２＝８０個になり，これがＢがもらうミカンの数になります。

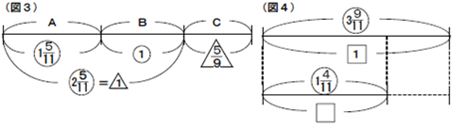
（２）こちらは和の線分図からもとにする量をそろえて，差の線分図で全体との関係をとらえてみましょう。ＡはＢをとおくと１＋１＝２にあたり，ＣはＡ＋Ｂをとおくと─になります。和の線分図で表せば図３のようになります。Ｃの色紙の枚数をマルで表すと２×＝１になります。全体の割合は２＋１＝３になり，これをもとにしたときの線分図を書くと図４のようになります。Ａの割合は１÷３＝になります。