第3回　分配算・差分け算｜線分図の究極奥義｜中学受験！パパとママの勉強部屋

第3回　分配算・差分け算

斎藤講師（鉄人会スーパープロ家庭教師）

　今回は決められた割合にしたがってお金などを分配する問題を考えます。その中で，もとにする量（基準量）が同じ問題だけを取り上げますが、これはもとにする量（基準量）が異なる問題への基礎となるとらえ方ですから、しっかりと理解するようにしましょう。

　線分図のとらえ方は第１回と同じになり、考え方は第２回の相当算と同じになります。割合関係を和の線分図や差の線分図に表しながら、実際の単位がある量がどれだけの割合にあたるのかを求めればよいのです。

　差の線分図は書ける人が多いと思うので、差の線分図の方がとらえやすい問題を除いてはできるだけ和の線分図でとらえてみます。ここに出てくる問題は、割合関係を比に表して解くこともできます。しかし、比を最初から使おうとするのではなく、問題文をそのまま線分図に表せるように練習してください。比でとらえるのは線分図に表してからでも遅くはありません。最終的には比にたどり着きますが、理解できないのにもかかわらず、早くできるからという理由で比を使って教えたり考えようとするのは、かえって理解をさまたげることにもなります。

　割合で分からないから比で解くのだという意見あるかもしれませんが、割合が理解できないと比は理解できません。多くの指導内容でも必ず割合の後に比が出てくることからも分かります。個人的な体験からすると、割合で解ける問題は割合で解いてしまえばいいと思います。テストでは制限時間の関係で、速く解けるようになることが求められるので、比が必要ないとは思いません。しかし、あくまで理解することのほうが優先されるべきだと思います。割合を十分理解していれば、自然に少しずつ比で解くようになっていきます。

［例題１］分配算-余りの出ない割合関係
次の問いに答えなさい。

（１）兄弟が父からもらった３０００円のおこづかいを分けようと思います。兄が弟の４倍になるように分けると、兄と弟がもらうお金はそれぞれ何円ですか。
（２）６０枚の折り紙があります。姉が妹の倍の枚数をもらうとき、姉と妹はそれぞれ何枚もらうことになりますか。
（３）２．７の水をコップでくみ出します。大きいコップでちょうど２杯くみ出したあと、小さいコップでちょうど４杯くみ出すとなくなりました。小さいコップは大きいコップの４０％の大きさです。大きいコップと小さいコップはそれぞれ１杯で何ｍずつくめますか。

［解説］
（１）これは整数の割合とみることができます。もとにする量は弟のもらうお金です。３０００円が弟のおこづかいの５倍にあたるので、弟は３０００÷５＝６００円、兄は３０００-６００＝２４００円をもらいます。

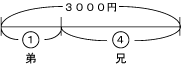
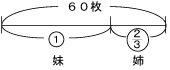
（２）もとにする量は妹のもらう枚数です。６０枚の折り紙が妹の１倍にあたるので、妹は６０÷１＝３６枚、姉は６０-３６＝２４枚をもらいます。

（３）もとにする量は大きいコップ１杯の容積です。小さいコップは大きいコップの４０％＝の割合です。すると、２．７＝２７００ｍが１×２＋×４＝３にあたるので、大きいコップは２７００÷３＝７５０ｍ、小さいコップは７５０×＝３００ｍです。

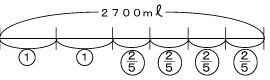
［練習１］（解答はこの回の最後にあります。）
次の問いに答えなさい。（必ず線分図を書くようにしましょう）

（１）ある日の昼の時間が夜の時間の１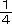になりました。昼の時間は何時間何分ですか。
（２）ある日、まり子さんたちは、子ども１０人と大人４人で遊園地に行きました。入園料は子ども１人が大人１人の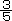とが同じ料金でした。まり子さんたちの入園料は全部で３５００円でした。子ども１人の入園料はいくらですか。

［例題２］分配算-余りの出る割合関係
次の問いに答えなさい。

（１）整数Ａから整数Ｂをひくと７００になり、ＡをＢでわると商が１５で余りが２８になります。整数Ａはいくらですか。
（２）兄弟２人でためた貯金が８７００円になりました。兄は弟の３倍より２４００円少なくなるよう分けると、兄がもらうお金は何円ですか。
（３）Ａ，Ｂ，Ｃの３人の持っているおこづかいの額は，ＡはＢより１２００円多く、ＢはＣの1.４倍より４００円少ない額です。３人の持っているおこづかいの合計が６１００円のとき、Ｂが持っている金額を求めなさい。１７００円

［解説］
（１）ここでは差が分かっているので、和の線分図より差の線分図（図１）の方がとらえやすいでしょう。「ＡをＢでわると商が１５で余りが２８」ということは、ＡはＢの１５倍より２８多いということになります。線分図から７００-２８＝６７２が１５-１＝１４にあたることが分かります。このことから、整数Ｂは６７２ ÷１４＝４８となり、整数Ａは４８＋７００＝７４８です。

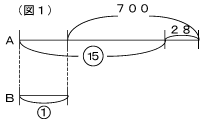
（２）これは和が分かっているので、和の線分図（図２）でとらえましょう。兄は弟の３倍に２４００円足りないので、あと２４００円あればちょうど３倍になります。８７００＋２４００＝１１０００円が１＋３＝４にあたることが分かります。弟のもらうお金は１１１００÷４＝２７５０円になり、兄がもらう金額は８７００-２７５０＝５９５０円になります。

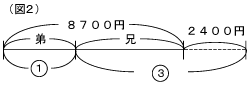
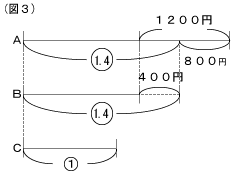
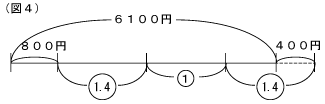
（３）おこづかいがもっとも少ないＣをもとにして考えます。Ｃをもとにすると、ＡはＣの１．４倍より１２００-４００＝８００円多くなります。これは差の線分図（図３）でとらえると分かりやすくなります。和で表すときは、Ｃを真ん中するととらえやすくなります。（図４）６１００-８００＋４００＝５７００円が１＋１．４＋１．４＝３．８にあたるので，５７００÷３．８＝１５００円がＣのおこづかいです。Ｂのおこづかいは１５００×１．４-４００＝１７００円になります。

［練習２］（解答はこの回の最後にあります。）

（１）２つの整数Ａ，Ｂがあり、Ａの２倍とＢの和は２２０７です。また、ＡをＢでわると、商は５であまりは２３になりました。整数Ａ，Ｂはそれぞれいくつですか。
（２）７００枚の紙を，さとし君、よしお君、たける君の３人に配りました。さとし君はよしお君より１７枚多く、たける君はよしお君の１．２倍より１１枚多くもらいました。３人はそれぞれ何枚もらいましたか。
（３）Ａ，Ｂ，Ｃ，Ｄ４人のおこづかいについて次のことが分かっています。ＡはＢのお金の２倍より２００円多い。ＢはＤより５００円多い。ＣはＡより１１００円少なく、Ｄの３倍より１００円少ない。４人のおこづかいの合計は３０００円。このとき、４人の所持金はそれぞれいくらですか。

［例題３］余りの出る相当算
次の問いに答えなさい。

（１）Ａ，Ｂの２種頬のセーターがあります。ＡはＢよりも３５００円高く、ＢはＡの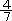よりも８００円安くなっています。Ｂのセーターは何円ですか。
（２）ＢはＡより３６０円少なく、ＡはＣより４５０円多く持っています。Ｃが持っているお金は３人の合計の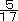にあたります。３人の持っているお金はそれぞれ何円ですか。

［解説］
（１）ここは差が分かっているので差の線分図でとらえましょう。図１のように表せば、３５００-８００＝２７００円が１-＝にあたることが分かります。このことから、Ａは２７００÷＝６３００円になり、Ｂの値段は６３００-３５００＝２８００円になります。

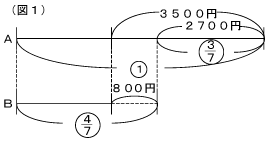
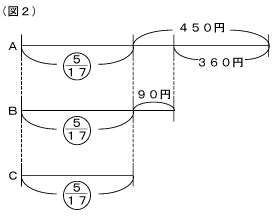
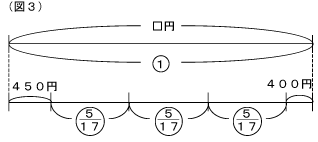
（２）一見すると差の線分図を利用した方がよさそうに見えますが、全体の合計金額をもとにしているので、相当算として和の線分図に持ち込んだほうがいいでしょう。しかし、３人の差をとらえるには差の方が分かりやすいので、ここでも両方の線分図で表してみましょう。差の線分図（図２）から、ＢはＣより４５０-３６０＝９０円多いことが分かります。和の線分図（図３）ではやはり、Ｃを真ん中にして線分図を書きます。前回の相当算の時と同じようにして考えれば、４５０＋９０＝５４０円が１- ×３＝にあたることが分かります。全体の合計金額は５４０÷ ＝４５９０円になります。Ｃのお金は４５９０＝１３５０円Ａは１３５０＋４５０＝１８００円、Ｂは１３５０＋９０＝１４４０円になります。

［練習３］（解答はこの回の最後にあります。）

（１）４つの数Ａ，Ｂ，Ｃ，Ｄを加えると１８０になり、Ａの５倍、Ｂの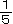、Ｃに５を加えた数、Ｄから５をひいた数はみな等しくなります。Ａはいくつですか。
（２）Ａ，Ｂ，Ｃ３人の所持金を比べると、ＡはＢよりも２００円多く、ＢはＣよりも３００円多く持ってました。また、Ｃの持っていたお金は３人の持っていたお金の和の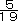でした。Ａの持っていたお金はいくらですか。