第2回　割合の線分図｜線分図の究極奥義｜中学受験！パパとママの勉強部屋

第2回　割合の線分図

斎藤講師（鉄人会スーパープロ家庭教師）

　「基準量」とは割合の「もとにする量」に当たります。割合についてはもうすでに理解しているという人がいるかもしれませんが、一応確認のために割合の考え方をまとめておきましょう。

　割合とはある量を１とおいて、他の量の大きさをはかったものです。１とおいた量のことをもとにする量（基準量）、他の量のことを比べられる量（比較量）といいます。

　たとえば、あなたが世界の王になったものとします。世界の王になれば何でも自分の好きなように決めることができます。そこで、あなたは自分の身長を１として、他の人の身長の大きさを表すというきまりをつくりました。すると、他の人の身長はすべてあなたの身長がもとになるので、あなたより大きい人は１より大きくなるでしょう。小さい人は１より小さくなるでしょう。
そして、大部分の人の身長は整数ではなく、小数や分数になります。

　あなたのお父さんが１.２になったとすれば、それはお父さんの身長があなたの１.２倍であることを表しています。１.２倍は分数にして倍と表しても同じことです。このとき、１より大きい場合は「～倍」という単位がありますが、１より小さい場合は「～倍」とはいえません。なぜなら，「～倍」というのは大きくなるという意味をもつために，小さくなる場合には使えないからです。「０.５倍」などというときがありますが、これは言葉の誤用です。習慣として許されているだけです。つまり、割合を考えるとき、１より大きくなる場合は「～倍」という単位をつけてもよいが、１より小さい場合、分数や小数で表された割合には単位がないことになります。

　それでは１より小さい場合はどのように表せばいいのでしょうか。分数や小数で表すこともできますが、そうすると単位をつけることができません。しかも、分数や小数ではきたない数になるのであつかいにくくなることがあります。そこで、ふつうは百分率や歩合で表します。

　百分率とはもとにする量を１００とおいたものです。歩合はもとにする量を１０とおいたものです。右の表のア～ナまでの空らんを埋めてみましょう。（この解答は省略します）

　割合の線分図は差の線分図です。それは割合が２つの量を比べていることからも分かります。例題を解きながら割合の線分図を学習していきましょう。ただし、この講座は線分図のとらえ方を中心とした内容ですから、割合の公式や求め方などはすでに理解しているものとして進めていきます。

［例題１］割合の３用法-百分率・歩合
Ａの身長は１５０ｃｍ、Ｂの身長は１２０ｃｍです。このとき、次の問いに答えなさい。
（１）Ｂの身長を１と表すとき、Ａの身長はいくつになりますか。分数と小数で答えなさい。
（２）Ａの身長を１と表すとき、Ｂの身長はいくつになりますか。百分率と歩合で答えなさい。

［解説］
この講座では割合の線分について、次のようなきまりをつくることにします。
（ア）分数・小数の割合には必ずマル囲い，サンカク囲いなどをする。
（イ）囲う記号の順番はマル→サンカク→シカク→ギャクサンカク→カッコとする。
（ウ）割合は線の下に、実際の単位がある量を線の上に書く。
（エ）もとにする量を上に、比べられる量を下にして差の線分図を書く。
（オ）問題文の中に出てくる百分率や歩合は分数・小数に表してから線分図に書く。
　割合でもっとも大切なことは「もとにする量」がはっきりと分かるようになることです。これがわかるまではあまり難しい問題に取り組まない方がよいでしょう。

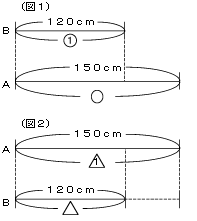
（１）Ｂの身長を１とおけば、Ａの身長は１より大きい数で表されるので、これはＡの身長がＢの身長の何倍かを求めることと同じです。きまりにしたがって線分図に表すと図１のようになります。

（２）Ａの身長を１とおけば、Ｂの身長は１より大きい数で表されるので、これはＡの身長がＡの身長のどれだけの割合かを求めることと同じです。きまりにしたがって線分図に表すと図２のようになります。

［練習１］（解答はこの回の最後にあります。）
次のをうめなさい。（必ず線分図を書くようにしましょう）

（１）Ａの体重は５６ｋｇ，Ｂの体重は３５ｋｇです。Ａの体重に対するＢの体重の割合を百分率で表すと％です。

（２）ｋｇの２４％は３６０ｇです。

（３）６００円の２割５分は円の７.５％にあたります。

［例題２］割合の差と相当算
次の問いに答えなさい。

（１）持っているおこづかいのうち、Ａ店で全体の、Ｂ店で全体のを使いました。Ａ店とＢ店で使ったお金の差は１５０円でした。はじめにおこづかいは何円ありましたか。

（２）容器に砂糖が入っています。この容器に入っている砂糖の重さのを使うと容器ごとの重さは６７０ｇになり、を使うと容器ごとの重さは３７０ｇになります。入れ物の重さは何ｇですか。

［解説］
　分数や小数、簡単な問題でも割合の線分図を書くようにしましょう。計算でできるような問題でも線分図を書くことが大切です。簡単な問題は計算でやればよいというのはテストのときの話です。これは面積図にもいえることですが、基本的な問題を線分図で表すことができないのに、難しい問題を線分図でとらえることなどできるわけがありません。本当に線分図を使いこなせるようになりたいのなら、なんでも線分図で表してみるくらいの気持ちが必要です。
　相当算では線分図を左からも右からも書くことがあります。どちらがいいかはそのときの問題によりますが、原則として左から書いていき、この例題の（２）や損益算などの差を中心にして考える問題は右から書いていきます。

（１）とはどちらも全体のおこづかいをもとにしています。そして、の方がのよりも１５０円多いということも通分して比べれば分かります。つまり、のなかにはと１５０円が含まれていることになります。それを差の線分図を利用して右図のように表します。１５０円は-＝にあたるので、１５０÷＝＝１,５００円になります。

（２）もとにする量は入れ物に砂糖をいっぱいにいれたときの砂糖の重さです。入れ物の重さは含めないので注意しましょう。６７０?３７０＝３００ｇの重さが-＝にあたるので、?は３００÷＝７２０円になります。

［練習２］（解答はこの回の最後にあります。）
（１）あるお店では，ペン１本は所持金のの金額で、ノート１冊は所持金のの金額でした。ペン１本とノート１冊の金額の差は７５円でした。ノート１冊の値段は何円ですか。

（２）石油が入っているカンがあります。全体のを使ったときの重さをはかると１２.８ｋｇでした。また、全体の─を使ったときの重さをはかったら８.４ｋｇでした。このカンだけの重さは何ｋｇですか。

［例題３］余りの出る相当算
次の問いに答えなさい。

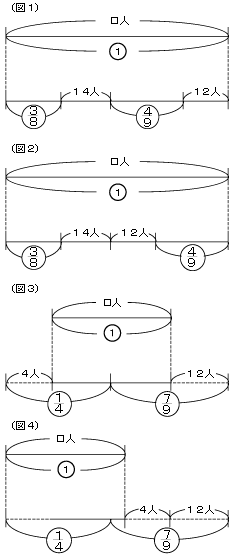
（１）ある学校では、男子は全体のより１４人多く、女子は全体のより１２人多くなっています。生徒全体の人数は何人ですか。

（２）ある学校の入学試験で、合格者数は受験者数のよりも４人少なく、不合格者数は受験者数のよりも１７人少なかったそうです。受験者数の総数は何人ですか。

［解説］
　ここでは「より多い」と「より少ない」の表し方を考えましょう。多い・少ないは割合と同じように、大小２つの量があって、どちらをもとにするかで言い方がかわります。「より多い」という場合はほとんどそのまま線分図に表してかまいません。問題は「より少ない」の方です。　第１回の差の線分図の表し方のところで、「Ａよりだけ少ないＢ」を「Ｂより～多いＡ」と言いかえました。「少ない」が出てきたら、できるだけ「多い」とすることにより線分図に表しやすくなリました。もう一つは「少ない」を「足りない」とみて、不足部分を補う表し方です。（２）ではこの「足りない」として表してみましょう。

（１）割合部分と人数部分の表し方によって、線分図から分かることがかわってきます。図１のように表してしまうと、１４人と１２人のそれぞれの割合は分かりません。ところが、図２のように表せば、１４＋１２＝２６人が１-＝であることが分かります。このようにして、単位のある量どうしや割合どうしを和として表すことで、いっそう分かりやすくなります。２６÷＝１４４人が全校生徒です。