第1回 線分図のとらえ方
斎藤講師(鉄人会スーパープロ家庭教師)
中学受験の算数を学習するとき、だれでも一度は「線分図」ということばを耳にしたことがあるでしょう。そして、線分図を書いたことがない人はほとんどいないはずです。
しかし、これほどだれにでも馴染みがありながら、線分図の表し方についてスッキリとまとめられている参考書や教材はあまり見当たりません。
そこで、この講座を通して、実際の入試問題を解きながら、統一的な線分図の書き方と利用方法を身につけてもらいたいと思います。
ただし,ここで取りあげる線分図の表し方がすべてではありません。ものごとのとらえ方はいろいろ考えられます。ここでの学習を自分独自のとらえ方へと発展させることが最終的な目標です。
線分図は問題文に出てくる数を線の長さで表した図のことで、大きく分けると2種類しかありません。「和の線分図」と「差の線分図」です。
問題文を読んで
差が分かっているとき→差の線分図
和が分かっているとき→和の線分図
線分図を書こうとするとき、まずはこのように考えてみるのがいいでしょう。それから、差がダメなら和で表す、和がダメなら差で表す、というようにどちらも使いこなせるようにしていくことです。具体的な表し方はあとで説明します。
一般的な参考書や教材には差の線分図が中心になっています。和の線分図は、基本的には和一定のやりとり算のときだけにしか出てこないことが多いのですが、それ以外でも積極的に使っていくことで、いろいろな場面で役に立つことがあります。
それでは例題を解きながら、線分図の表し方を考えてみましょう。
[例題1]和差算
AとBの和が30で、AがBより4大きいとき、次の問いに答えなさい。
(1)AとBを差の線分図で表しなさい。
(2)AとBを和の線分図で表しなさい。
(3)AとBをそれぞれ求めなさい。
[解説]
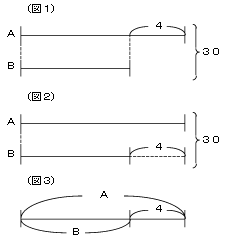
(1)差を表すときは、図1、図2のようにAとBを2本にする方法です。
これらのうち、図2は差ではなく、不足分を表す線分図です。図3は和が30ということを表せていません。ここでは図1を差の線分図ということにします。
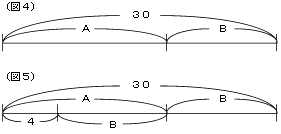
(2)和を表すときは、図4のようにします。これを図3とを組み合わせると図5となって、和と差を同時に表すことができます。
(3)図1から図5の中で、最も分かりやすいのは図6でしょう。これを見ればBは30から4を引いて2でわると求められることが分かります。また、Aを先に求めたいときは、図7のように、Bに4を加えればAになるので、34を2でわれば求められます。
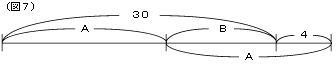
[解答]
(1)解説を参照 (2)解説を参照
(3)A…17、B…13
[練習1](解答はこの回の最後にあります。)
次の問いに答えなさい。(和の線分図と差の線分図をそれぞれ書いてみましょう)
(1)昼の長さが夜の長さよりも2時間30分長いとき、昼の長さは何時間何分ですか。
(2)平年のある日、1年の残りの日数を数えたら、今年の1月1日から今日までより45日少ないことが分かりました。今日は何月何日ですか。
[例題2]3量の和差算
1700円をA、B、Cの3人で分けるのに、AはBより250円多く、BはCより40円少なくなるように分けました。これについて、次の問いに答えなさい。
(1)A、B、C の所持金を差の線分図で表しなさい。
(2)A、B、C の所持金を和の線分図で表しなさい。
(3)A、B、C はそれぞれ何円ずつ受け取りますか。
[解説]
差の線分図と和の線分図を両方とも書くことができたでしょうか。はじめのうちは和の線分図が書けないと思います。その場合は無理に和の線分図を理解しようとする必要はありません。こうした別の表し方もあるということさえ分かればそれでいいのです。
3量以上の関係を考えるときは、最も小さい量にそろえるということが基本です。この問題の場合でも、最も所持金が少ないBをもとにして考えます。この問題のような大小関係だけではなく、これ以後の割合や比の関係を考えるときでも、基本的に小さい量をもとにして他の量を表した方が理解しやすいでしょう。
(1)3量以上の和と差の関係は、基本的には差の線分図でとらえた方が分かりやすいことが多いです。
(2) 和の線分図で表すとき、「BはCより40円少なくなる」という部分を「CはBより40円多くなる」というように考えます。「少ない」については回を追って説明していきます。
(3)和差どちらからも求められます。1700?(250+40)=1410の1410円がBの3倍にあたります。Bの所持金は1410÷3=470の470円です。Aの所持金は470+250=720の720円、C の所持金は470+40=510の510円です。
[解答]
(1)解説を参照 (2)解説を参照 (3)A…720円、B…470円、C…510円
[練習2](解答はこの回の最後にあります。)
(1)6年生はA、B、C、Dの4組あって、全部で200人です。A組はB組より3人多く、D組はC組より3人少なく、B組より1人少ないそうです。C組の人数は何人ですか。
(2)あやこさんの計算テストの成績は、2回目は1回目より6点多く、3回目は2回目より4点多く、1回目と3回目の合計は168点でした。1回目から3回目までの点数はそれぞれ何点でしたか。
◆練習問題の解答
(練習1)(1)13時間15分 (2)7月24日
(練習2)(1)52人 (2)1回目…79点、2回目…85点 、3回目…89点












